上机1:描述统计
一、上机目的
1.学会应用两种以上的方法完成描述统计学所学的统计量的计算程序;如列出数据的频数分布表;计算算术平均数、中位数、众数;计算全距、四分位差、标准差、方差等。
2.能够完成统计图的绘制(主要包括直方图、曲线图、饼形图、茎叶图);
3.能够撰写出规范的描述统计分析报告。
二、上机要求
1.前20分钟,主讲老师通过例题演示描述统计方法的应用;
2.中间70分钟,学生仿照演示题,独立做一个练习题目;期间老师课堂巡视,随时解决学生提出的问题;
3.后20分钟,每位同学将自己的计算结果,以Word形式,撰写成统计分析报告,老师给出是否合格的评价。
4.在完成练习题的时候,鼓励学生之间相互交流探讨;
5.鼓励学生尝试发现软件的新功能。
三、上机演示内容与步骤
下面给出的一个例题是来自SPSS软件自带的数据文件“Employee.data”,该文件包含某公司员工的工资、工龄、职业等变量,我们将利用此例题给出相关的描述统计说明,本例中,我们将以员工的当前工资为例,计算该公司员工当前工资的一些描述统计量,如均值、频数、方差等描述统计量的计算。计算各项描述统计量值的程序使用步骤如下:
步骤1:用SPSS打开已知的数据文件
选择菜单“File—>Open—>Data”,在对话框中找到需要分析的数据文件“SPSS/Employee data”,然后选择“打开”。

打开的数据文件显示如下:

步骤2:计算所要求的描述统计量值及频数分布
1.打开文件之后,选择菜单“Analyze—>Descriptive Statistics—>Frequencies”。见下图。
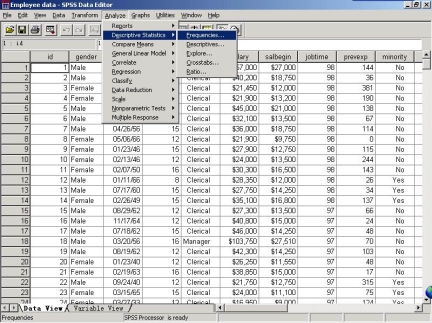
出现如下窗口之后,按后面的说明进行选项。
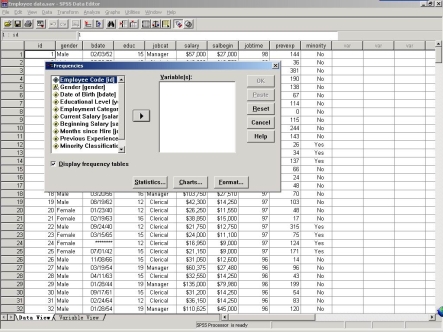
2.确定所要分析的变量
本例中假设要分析的变量是雇员的当前工资(Current Salary)。此时,要在“Frequencies对话框”中选中左侧列表框中的“Current Salary[Salary]”,之后点击列表框中间的箭头按钮,将变量Current Salary加入到右侧Variable(s)列表框中。然后,选择位于小窗口下端的“Display frequency tables复选框”,以确定要输出频数分布表。
3.选择所要计算的统计量
在变量选择确定之后,在同一窗口上,点击“Statistics”按钮,打开统计量对话框,如下图所示,选择统计输出选项。
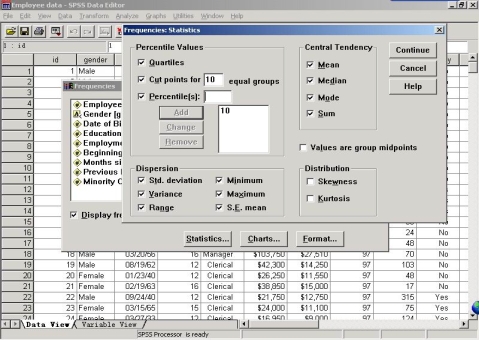
(1)Percentile Values 栏
��������Quartiles:显示25%,50%,75%的四分位数值
��������在Cut points for ___equal groups小框内,输入整数k时,表示将所选变量的数值从小到大划分为k等分,并将输出各等分点处的变量数值
��������在Percentile(s)右边的小框内,键入0~100间的一个数之后,单击Add按钮添加到下面的方框内,此操作过程可以重复。例如输入15,55,85时,输出结果将会显示15%,55%,85%百分位处的变量值。单击Change和Remove按钮可以修改或删除框内的数值
(2)Dispersion(离中趋势)栏
各统计量符号表示如下:Std deviation 标准差 ;Minimum 最小值;Variance 方差 ;Maximum 最大值;Range 极差
(3)Central Tendency(集中趋势)栏
各统计量符号表示如下:Mean 均值(算术平均数);Mode 众数;Median 中位数;Sum 总和
(4)Distribution(分布特征)栏
各统计量符号表示如下:Skewness 偏度;Kurtosis 峰度
步骤3:结果输出与分析
点击Frequencies对话框中的“OK”按钮,即得到下面的结果。
(1)Statistics(统计量)汇总表
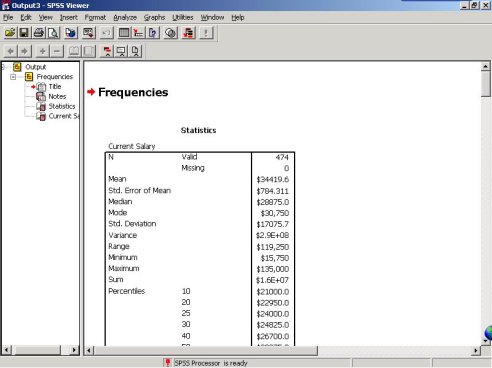
从Statistics表中可以清楚的看到当前薪水(Current Salary)的各项描述统计量的数值,这些数值是按我们上一步选定的计算统计量的要求而计算的。我们可以看出,要求计算的均值、众数、标准差、方差等都在其中,分别为$34419.6、$30750、$17075.7、$2.9E+08。
(2)Frequencies(频数)分布表
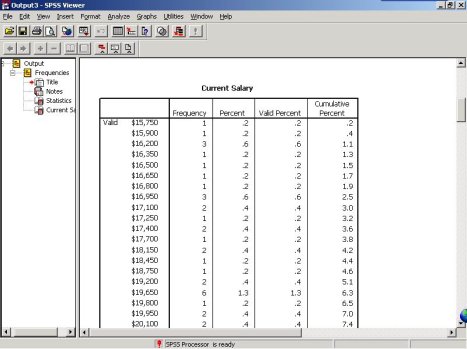
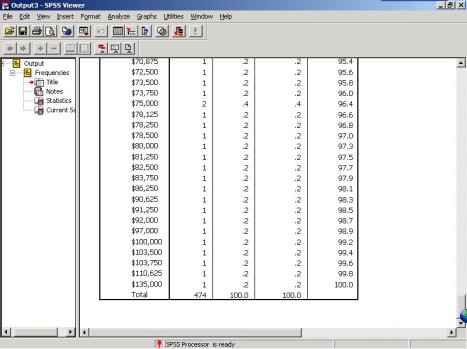
从Frequencies表中可以清楚的看到在不同薪酬档次上员工的人数、所占比例。例如,薪水为$15250的员工有1人,占所有员工的0.2%。
本处,没有对结果进行详细说明,希望同学们要学会解释所计算的结果。到此为止,有关描述统计量与频数分布的spss计算步骤演示完毕。下面我们给出另一种计算程序,希望同学们也熟练掌握。
描述统计-数据探索(Explore)方法
调用此过程可对变量进行更为深入详尽的描述性统计分析,故称之为探索分析。它在一般描述性统计指标的基础上,增加有关数据其他特征的文字与图形描述,显得更加细致与全面,对数据分析更进一步。
探索分析一般通过数据文件在分组与不分组的情况下获得常用统计量和图形。一般以图形方式输出,直观帮助研究者确定奇异值、影响点、还可以进行假设检验,以及确定研究者要使用的某种统计方式是否合适。
步骤1: 在打开的数据文件上,选择如下命令:选择菜单“Analyze—>Descriptive Statistics—>Explore”,打开Explore对话框。
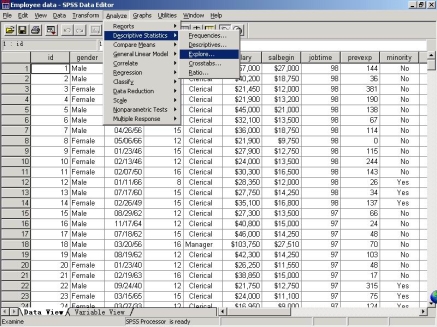
步骤2: 确定所要计算的变量及描述统计量
假定我们仍然研究的是前面给出的例题,想给出同样的计算结果。操作步骤如下:
(1) 选择要研究的变量。从左侧源变量清单中选择“当前工资(Current Salary)”移至Dependent List(因变量)框中,若此时单击OK,即可获得所有系统默认的选项下作出的描述统计量的结果。
(2)对数据分组。若想对数据先分组,然后再计算该变量的相关描述统计量时,则应从左侧源变量清单中选择一个或几个分组变量移至Factor List(因素)框,本例中,选择的分组变量是“雇员类别(Employment Category)”,若此时单击OK,即可获得因变量按各分组变量进行的各项系统默认的分组探索结果。
(3)选择想要计算的描述统计量。在出现如下小对话窗口(Explore:Statistics)后,需要进行选项,以说明对选择好的变量要计算的是哪些描述统计量值。其各项选择说明如下。
��������Descriptives:选择该选项则一次性地输出所有的描述统计量值,如算术平均值、中位数、众数、5%调整平均数、标准差、极差、方差等。因此不必逐一选择各个描述统计量
其他项目简单说明如下:Confidence Interval for Mean将显示总体均值的95%置信区间,95%为系统默认的置信概率。取值范围为1—99。
��������M-estimators:输出稳健极大似然估计量
��������Outliers:输出5个最大和最小的观测值
��������Percentiles:输出5%,10%,25%,50%,75%,90%,95%的百分位数
(4)对所要计算的变量的频数分布及其统计量值作图
打开“Plots对话框”,出现如下图形。对有关的部分选项说明如下:
① Boxplots(箱图)选项栏
��������Factor levels together:将每个因变量对于不同分组的箱图并列显示,利于比较各组在因变量同一水平上的差异
��������Dependents together:所有因变量生成一个箱图,这样可以比较分组变量同一水平上各个因变量值的分布情况
��������None:表示不显示箱图
② Descriptives栏
��������Stem-and-leaf:显示茎叶图
��������Histogram:显示直方图
③ 选中Normality plots with tests框中输出显示正态分布图形,同时输出Kolmogorov-Smirnov统计量中的Lilifors显著性水平
④ Spread vs. Level with Levene Test框输出散布-层次图,其中包括回归直线斜率以及方差齐次性的Levene检验。如果没有指定分组变量,那么此选项无效,其中:
��������None:表示不生成散布-层次图
��������Power estimation:转换幂值估计,表示对每一组数据产生一个中位数范围的自然对数与四分位范围的自然对数的散点图
��������Transformed:对原始数据进行转换,由用户在Power下拉框中指定幂变换使用的幂值,Power下拉框共有:三次方(Cube)、平方(Square)、平方根(1/Square root)、取对数(Logarithm)等
��������Untransformed:不对原始数据进行转换
步骤3: 结果的输出与说明
(1)Case Processing Summary表
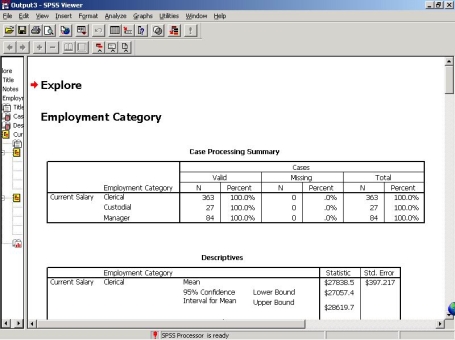
在Case Processing Summary表中可以看出Clerical个案363,Custodial个案27,Manager个案84,均无缺失值。
(2)Descriptives表
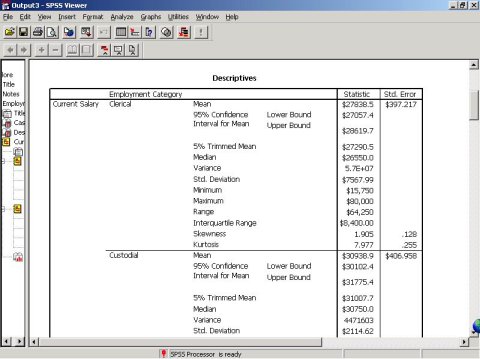
Descriptives表是Current Salary变量的分组描述统计结果。表的第一部分是Clerical薪水的统计,其中包括均数$27838.5,均数的标准误为$397.217,均数的95%置信区间为$27057.4—$29619.7,5%修正均数为$27290.5,中位数为$26550.0,方差为5.7E+07,标准差为$7567.99,最小值为$15750,最大值$80000,全距为$64250,四分位全距为$8400.00,偏度系数为1.905,偏度系数的标准误为0.128,峰度系数为7.977,峰度系数的标准误为0.255。
表的下面部分分别是Custodial和Manager的统计信息。
(3)不同职位员工薪水直方图显示
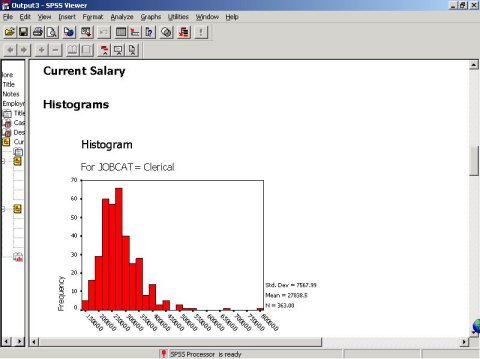
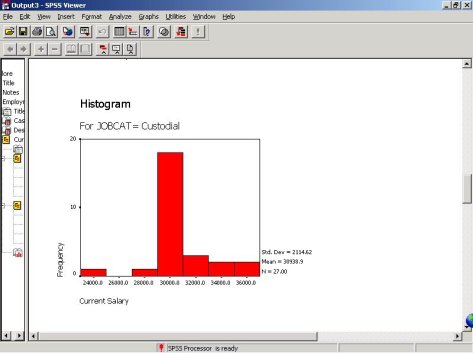
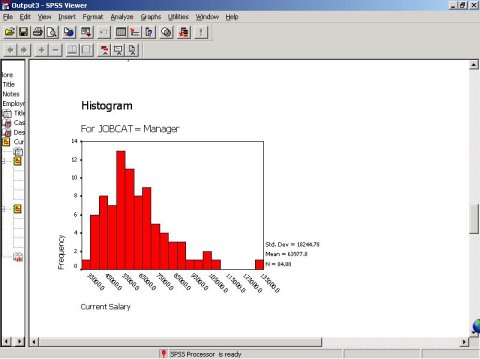
(4)茎叶图描述
茎叶图自左向右可以分为3大部分:频数(Frequency)、茎(Stem)和叶(Leaf)。茎表示数值的整数部分,叶表示数值的小数部分。每行的茎和每个叶组成的数字相加再乘以茎宽(Stem Width),即茎叶所表示的实际数值的近似值。
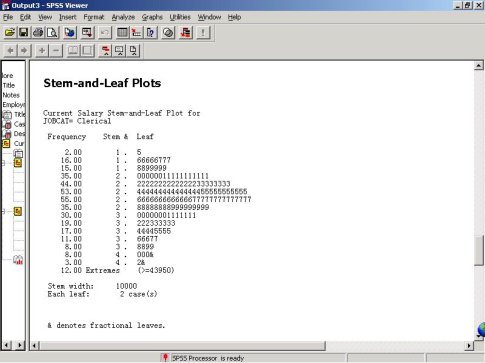
上面是Clerical的茎叶图。该图最后一行表示两个个案。以第一行数据为例,频数为2,茎为1,叶为0.5,茎宽为10000,表示有两个个案的薪水为1.5×10000=15000。
Custodial和Manager的茎叶图在此省略。
(5)箱图
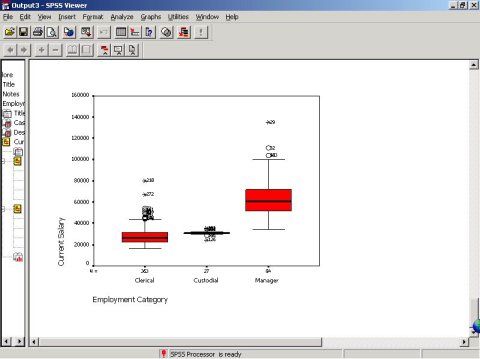
图中红色区域的方箱为箱图的主体,上中下3条线分别表示变量值的第75、50、25百分位数,因此变量的50%观察值落在这一区域中。
方箱中的中心粗线为中位数。箱图中的触须线是中间的纵向直线,上端截至线为变量的最大值,下端截至线为变量的最小值。
四、上机1报告概要
上机2:统计图的绘制
SPSS绘图功能很强,能绘制许多统计图形,这些图形既可以在统计分析过程中产生,也可以直接由Graphs图形菜单中所包含的一系列选项来实现。
一、上机目的
1. 学会利用统计图把统计资料所反映的数量变化趋势、分布状态和相互关系等情况形象直观地表现出来;
2. 学会对所制作的统计图进行阅读、比较和分析,从中发现数据所反映的社会经济现象与规律;
3. 要求掌握制作条形图、饼图、直方图、曲线图的方法;
二、上机演示内容与步骤
下面采用的数据文件同前例题,它是来自SPSS软件自带的数据文件Employee.data”,该文件包含某公司员工的工资、工龄、职业等变量,我们利用该数据文件学习统计图的绘制。
步骤1:用SPSS打开已有的数据文件
选择菜单“File—>Open—>Data”,在对话框中找到需要分析的数据文件“SPSS/Employee data”,并“打开”。
步骤2:绘制条形图(Bar Charts)
作图要求:以该数据为例,先按员工教育水平分类(教育水平是按接受教育的年限为主的),然后在分好的类别中,再按员工职业类别分类(经理、保管员、服务员),最后计算各种类别人员的平均工资水平并绘制条形图。作图步骤如下:
(1)打开文件并选择绘制条形图选项。
选择菜单“Graphs—>Bar”,打开Bar Charts(条形图)选择对话框,见下图。
出现下图所示之后,选择合适的命令选项,各项命令选项说明如下:
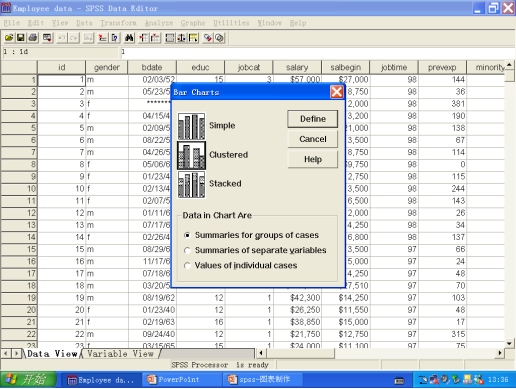
(2)命令选项的选择
① 条形图形状的选择-条形图图标说明
l Simple:将各类别数值用平行且等宽的条形简单地并列在一起的图形。
l Clustered:有两种以上分类的数据显示方式,首先将数据分为第一类,然后各类数据再进一步细分为第二类,并用两个以上的条形图并列来分别表示。
l Stacked(分段条形图):有两种以上分类的数据显示方式,首先将数据分为第一类,然后各类数据再进一步细分为第二类。作图时,以条形的全长代表分成的第一大类别,条形内部各段的长短代表第二类别的组成部分,各段之间是用不同的线条或颜色表示。
② 计算数据统计量的方式选择-Data in Chart Are
Ø������Summaries for groups of cases:先对所有数据分类,然后对每类创建条形图
Ø������Summaries of separate variables:对每个变量创建条形图
Ø������Values of individual cases:对每个数据创建条形图
(3)条形图变量及参数选择
在Bar Charts对话框中选定条形图类型后,单击Define按钮,打开条形图变量及参数选择对话框
(1)Category Axis:表示坐标轴上的分组变量(第一次分类的变量)。
(2)Define Clusters by:第二次分类的变量
(3)Bars Represent:确定条形图所显示的数值。有如下选项可供选择:
Ø������ N of cases:显示总的观测值数
Ø������% of cases:分组个数所占的比例
Ø������Cumulative n of cases:累计频数(按个数统计)
Ø������Cumulative % of cases:累计频率(按比例统计)
Ø������Other summary function:其他描述统计量
(4)条形图输出
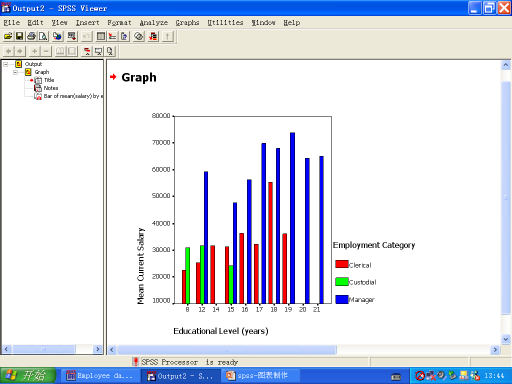
步骤3:绘制想通过饼形图(Pie Chars)来了解该公司各员工类别在公司总人数中所占的比例,员工类别构成比例。作图步骤如下:
(1)打开已有数据文件并选择绘制饼形图命令选项
选择菜单“Graphs—>Pie”,打开Pie Charts选择对话框。见下图,
(2)命令选项的选择
Data in Chart Are(图中数据的描述)
Ø������Summaries for groups of cases:根据分组变量先对所有个案进行分组,然后对分组个案创建图
Ø������Summaries of separate variables:对每个变量创建图
Ø������Values of individual cases:对每个个案创建图
(3)饼形图变量及参数选择
① Slices Represent:确定扇形片的代表含义。有如下选项:
Ø������ N of cases:总观测值
Ø������% of cases:分组个数所占的比例
Ø������Cumulative n of cases:累计频数
Ø������Cumulative % of cases:累计频率
Ø������Other summary function:其他统计量
② Define Slices by:确定扇形片代表的分类变量
(4)输出饼形图
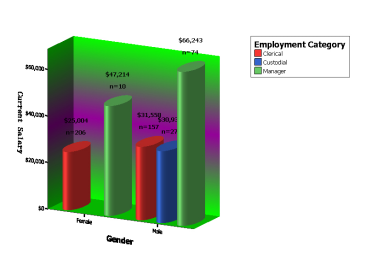
由饼形图可以看出,Clerical占了所有员工的75%多,Manager大概占了18%,其余为Custodial。
步骤4:绘制交互式条形图(Interactive Bar)
作图说明,想了解该公司接受不同教育年限的人数分布情况、了解不同性别平均收入水平情况,并通过交互式条形图加以显示。
(1)打开文件并调用交互式条形图绘制选项
选择菜单“Graphs—>Interactive—>Bar”,打开Create Bar Chart(创建条形图)对话框。在本例中,将Count变量拉入纵坐标轴,将Educational Level变量拖入横坐标轴。
(2)创建交互式条形图
l Assign Variables:用于设置变量和图类型
l Bar Chart Options:条形图选项
l Error Bars:误差条图
l Titles:标题选项
l Options:选项
(3)交互式条形图输出

从图中可以看出,在各个教育水平上的人数。
选择菜单“Graphs—>Line”,打开Line Charts(线图)选择对话框。
三、上机2报告概要
请作出下列图形,数据资料见下:
标题:婴儿母乳与配方奶日摄入量
日时间:2:10 5:30 9:20 12:00 15:30 19:10 21:05 23:50
母乳/配方摄入量:60/50 80/30 70/40 70/30 50/60 70/30 80/30 60/50
资料来源:婴儿健康指南,2003年。
上机3:点估计与区间估计
一、上机目的
1.熟悉点估计概念与操作方法;
2.熟悉区间估计的概念与操作方法;
3.学会进行总体均值、总体比率的区间估计。
二、上机演示内容与步骤
下面将学习“总体方差未知,置信度为95%下的区间估计”与“两个总体均值之差的区间估计(总体方差未知且不等)”等4种情形的操作。
情形1:总体方差未知,置信度为95%下的总体均值的区间估计
例题:为研究在黄金时段中,即每晚8:30-9:00内,电视广告所占时间的多少。美国广告协会抽样调查了20个最佳电视时段中广告所占的时间(单位:分钟)。请给出每晚8:30开始的半小时内广告所占时间区间估计,给定的置信度为95%。
操作程序:
步骤1:打开SPSS,按如下图示格式输入原始数据,建立数据文件:“电视广告所占时间.spss”。这里,time表示电视广告所占时间的变量。
步骤2:选择区间估计选项,方法如下:
选择菜单“Analyze—>Descriptive Statistics—>Explore”,打开Explore对话框。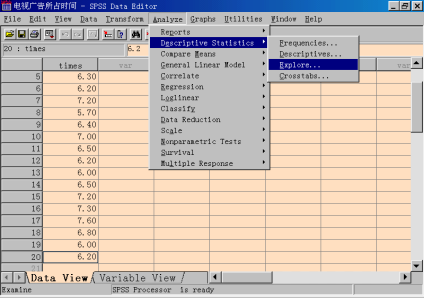
(2)从源变量清单中将“time”变量移入Dependent List框中。
(3)单击上图右下方的“Statistics”按钮打开“Explore:Statistics”对话框。
在Confidence Interval for Mean:的选项中,键入95%,表示计算选择的置信区间。完成后单击“Continue”按钮回到Explore窗口。
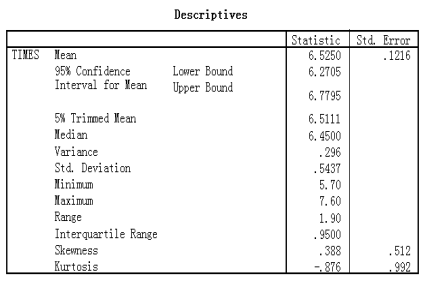
步骤3:计算结果简单说明
如上表显示。从上表“ 95% Confience Interval for Mean ”中可以得出,每晚8:30开始的半小时内广告所占时间区间估计(置信度为95%)为:(6.2705,6.7795),其中lower Bound表示置信区间的下限,Upper Bound表示置信区间的上限。点估计是:6.5250。
情形2:两个总体均值之差的区间估计(总体方差未知且不等)的情形
例题:The Wall Street Journal(1994,7)声称在制造业中,参加工会的妇女比未参加工会的妇女的报酬要多2.5美元。想通过统计方法,对这个观点是否正确给出检验。
假设抽取了15位女性工会会员与20位非工会会员女性报酬数据。要求对制造业中参加工会会员的女性报酬与未参加工会的女性报酬平均工资之差进行区间估计,预设的置信度为95%。
步骤1:打开SPSS,按如下图示格式输入原始数据,建立数据文件:“工会会员工资差别.spss”。这里,“会员”表示是否为工会会员的变量,y表示是工会会员,n表示非工会会员,“报酬”表示女性员工报酬变量,单位:千美元。
步骤2:计算两总体均值之差的区间估计,采用“独立样本T检验”方法。
选择菜单“ Analyze —> Compare Means —> Independent-Sample T Test”,打开Independent-Sample T Test对话框。
2.变量选择
(1)从源变量清单中将“报酬”变量移入Test Variable(s)框中。表示要求该变量的均值的区间估计。
(2)从源变量清单中将“会员”变量移入Grouping Variable框中。表示总体的分类变量。
步骤3:定义分组
单击Grouping Variable框下面的Define Groups按钮,打开Define Groups对话框。
在Group1中输入y,在Group2中输入n(y表示工会会员,n表示非工会会员)。完成后单击“Continue”按钮回到Independent-Sample T Test窗口。
步骤4:计算结果
单击上图中“OK”按钮,输出结果如下图所示。
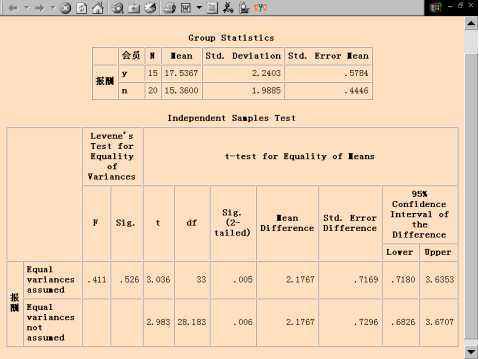
(1)Group Statistics(分组统计量)表
分别给出不同总体下的样本容量、均值、标准差和平均标准误。从该表中可以看出,参加工会的妇女平均报酬为17.5367,不参加工会的妇女平均报酬为15.3600。
(2)Independent Sample Test(独立样本T检验)表
��������Levene’s Test for Equality of Variance,为方差检验,在Equal variances assumed(原假设:方差相等)下,F=0.411,因为其P-值大于显著性水平,即:Sig.=0.526>0.05,说明不能拒绝方差相等的原假设,接受两个总体方差是相等的假设。
��������T-test for Equality of Means为检验总体均值是否相等的t检验,由于在本例中,其P-值小于显著性水平,即:Sig.=0.005<0.05,因此应该拒绝原假设,也就是说参加工会的妇女跟未参加工会的妇女的报酬有显著差异,从而说明参加工会的妇女比未参加工会的妇女的报酬要多。
情形3:单个总体均值的假设检验
例子:某种品牌的沐浴肥皂制造程序的设计规格中要求每批平均生产120块肥皂,高于或低于该数量均被认为是不合理的,在由10批产品所组成的一个样本中,每批肥皂的产量数据见下表,在0.05的显著水平下,检验该样本结果能否说明制造过程运行良好?
步骤1:判断检验类型
该例属于“小样本、总体标准差![]() 未知、原假设为
未知、原假设为![]() :μ=μ0,
:μ=μ0,![]() :μ≠μ0的总体均值”的假设检验。
:μ≠μ0的总体均值”的假设检验。
步骤2:软件实现程序
打开已知数据文件,然后选择菜单“Analyze—> Compare Means —> One-Sample T Test”,打开One-Sample T Test对话框。
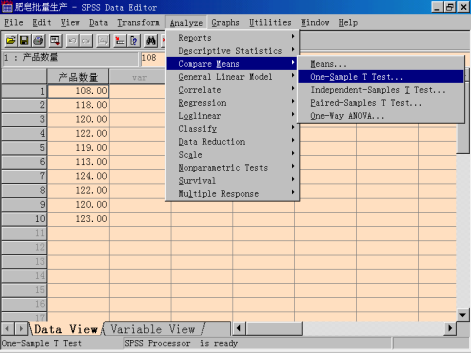
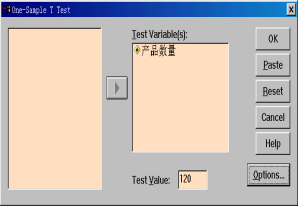
从源变量清单中将“产品数量”向右移入“Test Variables”框中。
②在“Test Value”框里输入一个指定值(即假设检验值,本例中假设为120),T检验过程将对每个检验变量分别检验它们的平均值与这个指定数值相等的假设。
“One-Sample T Test”窗口中“OK”按钮,输出结果如下图所示。
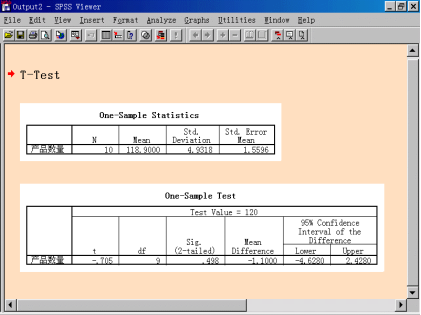
(1)“One-Sample Statistics”(单个样本的统计量)表
分别给出样本的容量、均值、标准差和平均标准误。本例中,产品数量均值为118.9000。
(2)“One-Sample Test”(单个样本的检验)表
表中的t表示所计算的T检验统计量的数值,本例中为-0.705。
表中的“df”,表示自由度,本例中为9。
表中的“Sig”(双尾T检验),表示统计量的P-值,并与双尾T检验的显著性的大小进行比较:Sig.=0.498>0.025,说明这批样本的平均产量与120无显著差异。
表中的“Mean Difference”,表示均值差,即样本均值与检验值120之差,本例中为-1.1000。
表中的“95% Confidence Internal of the Difference”,样本均值与检验值偏差的95%置信区间为(-4.628,2.428),置信区间包括数值0,说明样本数量与120无显著差异,符合要求。
情形4:两总体均值相等的假设检验(两总体标准差未知但相等)
例子:为节约系统分析员对某信息系统设计、开发、实现所需的时间而开发了一个计算机软件包。为评价新软件包的作用,随机地抽取24名系统分析员并平均分为两组,一组采用当前软件包,一组使用新软件包,对他们使用软件来开发某信息系统所花费的时间调查如下表。是否可以说新软件缩短了研发时间?
步骤1:判断检验类型
该例题属于两个正态总体标准差未知但相等时,均值的检验(双侧检验),假设为:![]() :
:![]() ,
,![]() :
:![]() 。
。
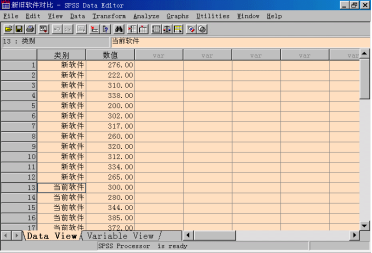
步骤2:上机程序
(1)独立样本的T检验
首先打开已有数据文件,然后选择菜单。“Analyze—>Compare Means—>Independent-Sample T Test”,打开Independent-Sample T Test对话框。
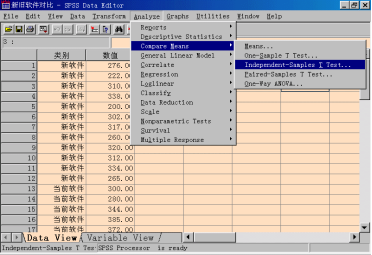
(2)选择所要检验的变量

①从源变量清单中选择数值型变量“数值”移入Test Variable(s)框。
②选择分组变量“类别”移入Grouping Variable框中。
步骤4:计算结果说明
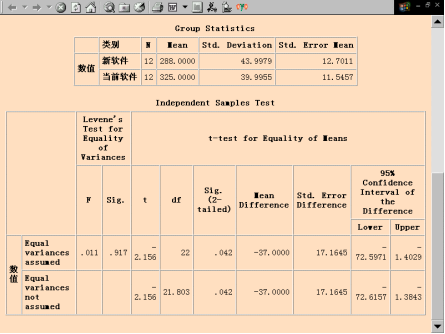
(1)Group Statistics(分组统计量)表
分别给出样本的容量、均值、标准差和平均标准误。采用新软件所费平均时间为288小时,当前软件为325小时。
(2)Independent Sample Test(独立样本T检验)表
Levene’s Test for Equality of Variance,为方差齐次性检验,在Equal variances assumed(等方差假设)下,F=0.011,显著性概率Sig.=0.917>0.05,说明方差相等。
T-test for Equality of Means为均值相等的t检验,t分布的双尾显著性概率Sig.=0.042›��������0.025,因此应该不拒绝原假设,所以认为使用当前软件和新软件开发信息系统所用时间没有显著的差异。
上机4:相关分析
一、上机目的
1.掌握相关分析的基本概念与公式;
2.学会相关分析的上机操作步骤。
衡量事物之间,或称变量之间线性相关程度的强弱并用适当的统计指标表示出来,这个过程就是相关分析。相关分析的方法较多,比较直接和常用的一种是绘制散点图。图形虽然能够直观展现变量之间的相关关系,但不很精确。为了能够更加准确地描述变量之间的线性相关程度,可以通过计算相关系数来进行相关分析。相关系数是衡量变量之间相关程度的一个量值。如果相关系数是根据总体全部系数计算的,称为总体相关系数,记为![]() ;如果是根据样本数据计算而来的,则称为样本相关系数,记为
;如果是根据样本数据计算而来的,则称为样本相关系数,记为![]() 。在统计学中,一般用样本相关系数
。在统计学中,一般用样本相关系数![]() 来推断总体相关系数。
来推断总体相关系数。
设两总体变量为(X,Y)。设![]() 为随机抽样值。它们的一组观察数据为:
为随机抽样值。它们的一组观察数据为:![]() ,
,![]() ,……,
,……,![]() 。
。
样本相关系数(Correlation coefficient)指标。定义:
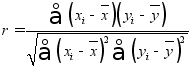
称![]() 为:Pearson’s correlation coefficient。
为:Pearson’s correlation coefficient。
二、上机演示内容与步骤演示
例题:道琼斯工业指数(DJIA)和标准普尔500种股票指数(S&P),都是用来衡量股票市场变动情况的。DJIA是基于30个大公司的股价变动,而S&P是基于500种股票股价的变动。有人说后者衡量股市的变动情况更合适,因为它包含的股票数量多。下面给出两者的数据表化,计算它们的相关系数。
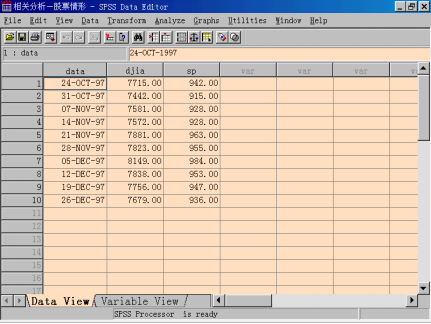
步骤1:打开相关分析命令
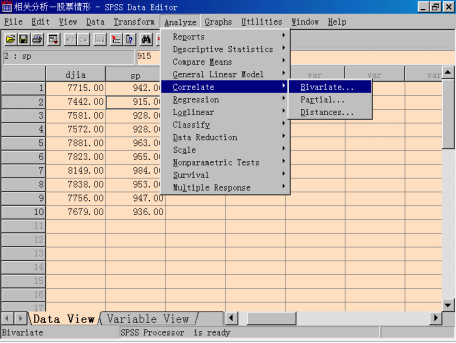
选择菜单“Analyze—>Correlate—>Bivariate”,打开Bivariate Correlation对话框。
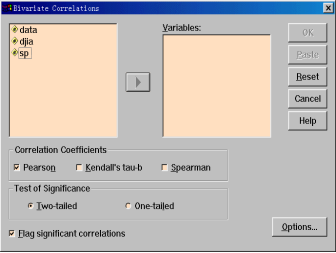
步骤2:变量选择
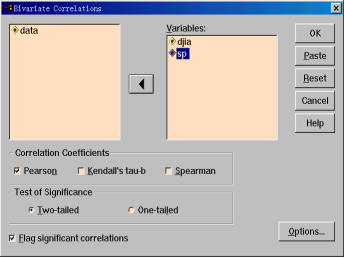
1.从源变量框中将djia和sp移入Variables框中。
2.在Correlation Coefficients框中选择相关系数的类型,共有3种:Pearson简单相关系数、Kendall’s tua-b和Spearman等级相关系数,本例选用Pearson系数。
3.在Test of Significance框中可选择相关系数的单侧(One-tailed)或双侧(Two-tailed)检验,本例选择双侧检验。
4.本例中还选中了Flag significations correlations选项,它表示相关分析结果中将不显示统计检验的相伴概率,而以星号(*)表示。一个星号表示当用户指定的显著性水平为0.05时,统计检验的相伴概率值小于等于0.05,即总体无显著线性相关的可能性小于等于0.05;两个星号表示当用户指定的显著性水平为0.01时,统计检验的相伴概率值小于等于0.01,即总体无显著线性相关的可能性小于等于0.01。显然,两个星号比一个星号的检验更准确。
步骤3:结果输出及相关矩阵分析
单击“OK”按钮,输出结果如下图所示。

1.表下对表中双星号标记的相关系数作出注释,即在显著性水平在0.01下,认为标记的相关系数是显著的。
2.表中显示djia和sp的相关系数为0.995,表明这两个指数之间具有非常密切的关系。
上机5:回归分析
一、上机目标
1. 学会在SPSS上实现一元及多元回归模型的计算与检验;
2.学会回归模型的散点图与样本方程图形;
3.学会对所计算结果进行统计分析说明。
二、上机要求
要求上机前,了解回归分析的如下内容
(1)参数α、β的估计
采用最小二乘法,使随机误差(残差)平方和为最小,即![]() 。可求得
。可求得
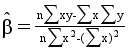
![]()
于是回归方程是:![]() 。
。
(2)回归模型的检验
① 回归系数β的显著性检验(t-检验)。假设为![]() :
:![]() ,
,![]() :
:![]() ,检验统计量为
,检验统计量为 ![]() 。
。
②回归方程显著性检验(F-检验)。假设为![]() :线性关系不显著。
:线性关系不显著。
三、上机演示内容与步骤
(一)一元线性回归
一元线性回归分析是在排除其他影响因素或假定其他影响因素确定的条件下,分析某一个因素(自变量)是如何影响另一事物(因变量)的过程,所进行的分析是比较理想化的。其实,在现实社会生活中,任何一个事物(因变量)总是受到其他多种事物(多个变量)的影响。
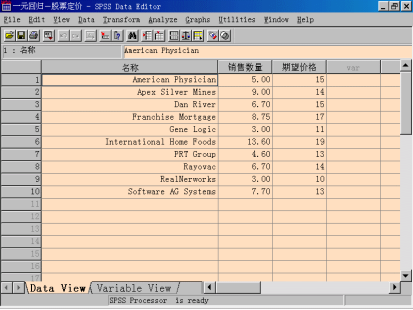
步骤1:打开回归模型程序
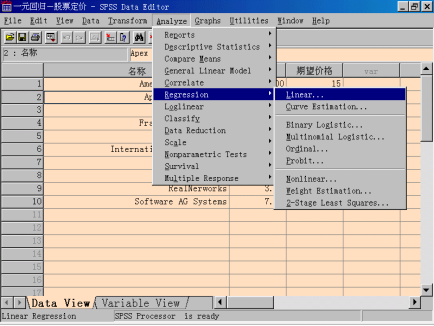
选择菜单“Analyze—>Regression—>Linear”,打开Linear Regression对话框。
步骤2:变量选择
(1)从源变量清单中选择数值型变量“期望价格”作为因变量移入Dependent框中。
(2)选择“销售数量”作为自变量移入Independent(s)框中。
(3)在Method框中选择Enter选项,表示所选自变量全部进入回归模型。
步骤3:结果输出及分析
单击“OK”按钮,输出结果如下图所示。
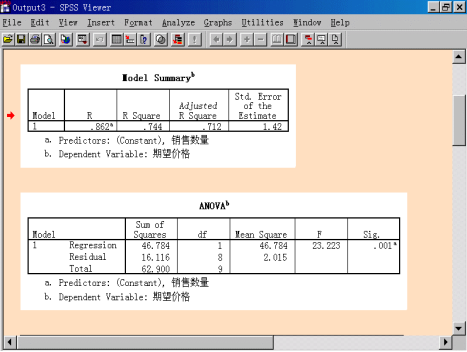
(1)模型概述(Model Summary)表
表中显示,相关系数R=0.862,判定系数![]() =0.744,调整后的判定系数
=0.744,调整后的判定系数![]() =0.712,估计标准误为1.42。由此说明“期望价格”与“销售数量”有比较显著的线性相关关系。
=0.712,估计标准误为1.42。由此说明“期望价格”与“销售数量”有比较显著的线性相关关系。
(2)方差分析(ANOVA)表
① Sum of Squares,表示项目平方和,如表所示,Regression:回归平方和为46.784,Residual:残差平方和为16.116,Total:总平方和为62.900;
② df,表示自由度,分别为1、8、9;
③ Mean Square,表示均方和,分别为46.784和2.015;
④ F,表示统计量值,为23.233;
⑤ Sig.,表示F分布的P-值,Sig.=0.001<0.05,因此拒绝原假设,说明回归方程获得通过。
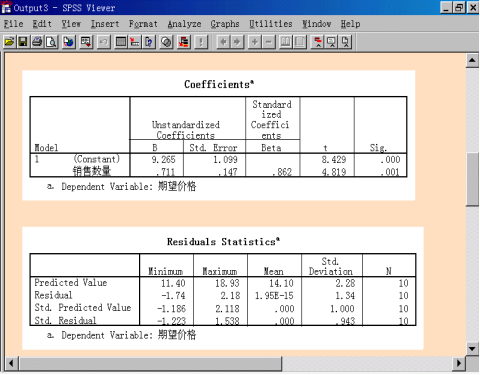
(3)模型系数(Coefficients)表
表中显示回归模型中的回归系数:Constant(常数项)为9.265,自变量系数为0.711,可知回归方程为:
期望价格=9.265+0.711×销售数量
回归系数的显著性水平为0.000和0.001,表明两变量分别是统计显著的,回归变量引入是有效的。
(4)残差统计(Residuals Statistics)表
表中依次列出预测值、非标准化残差、标准预测值、标准化残差。
横行依次列出上述各值的最小值、最大值、均值、标准差以及参与计算的观测量数目N。
(二)交互式散点图
步骤1:调用散点图程序
选择菜单“Analyze—>Interactive—>Scatterplot”,打开Create Scatterplot对话框。
步骤2:选择变量
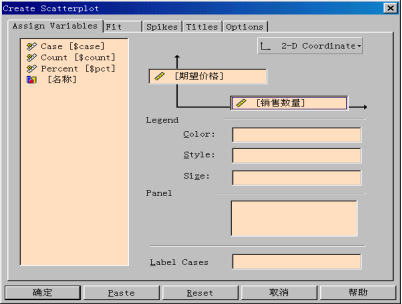
(1)从源变量框中将“期望价格”拖入竖坐标轴。
(2)从源变量框中将“销售数量”拖入横坐标轴。
步骤3:散点图结果输出及分析单击“确定”按钮,输出结果如下图所示。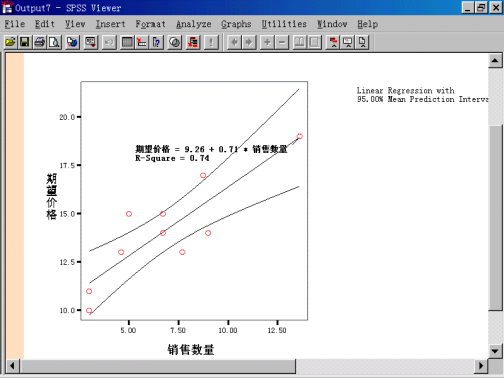
(1)从图中可以看出“期望价格”和“销售数量”之间的关系,方程式为:
期望价格=9.26+0.71×销售数量
(2)样本决定系数R-Square=0.74。
1